トップページ＞熱流体事例＞　機能別及び検証事例＞乱流事例＞高々度テスト設備のための流れ計算

高々度テスト設備のための流れ計算

概要：２次元乱流２相流空気－パーティクル流れの計算,円筒座標系,球状パ-ティクルdrag法の２相運動量交換モデル,乱流モデル：K-ε乱流モデル、Chen-WoodとMostafa-MongiaのK-ε乱流モデル,放物型計算法が使われ、計算は直径の70倍の距離まで計算されている（ここまで流れは十分発達してる）

・軌道へ衛星を打ち上げるアポジキックモーターRAFAELの開発は、ノズルの拡大部における十分な流れの膨張を地表面上の大気圧下でテストできるような、超音速ディフューザを備えた高々度テスト設備の設計を必要とした

・超音速ディフューザの能力は、その配置に敏感に依存する

・実験は粘性、乱流、圧縮性、亜音速、遷音速、超音速流れにおける複雑な現象の存在を示唆している

・PHOENICSはこれらの実験をシミュレートするために使用された

・サブスケールモデルテスト実験での検証の後、フルサイズモデルでの超音速ディフューザの設計過程を助けるためにPHOENICSが使用された

要点：以下のような仮定で行った

・２次元軸対称座標系

・定常計算

・単相流（排気ガスは凝縮した固体相を持っているが、その割合は1％程度なので無視）

・完全な乱流状態を仮定し、K-ε乱流モデルを使用

・乱流が流れに及ぼす影響を調べるため、いくつかの計算は乱流モデルなしで実行された

結果：

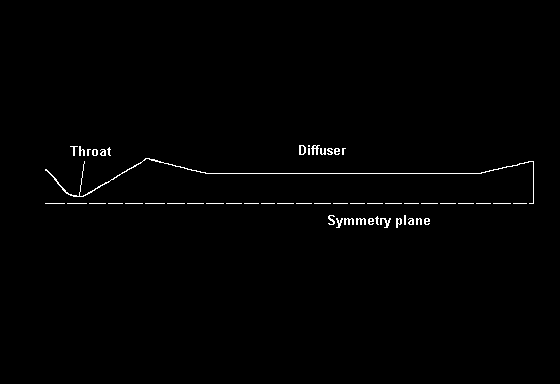
図１．ディフューザ形状

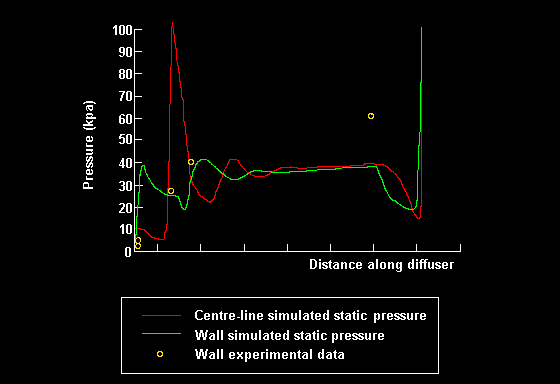
図２．静圧の計算値と測定値

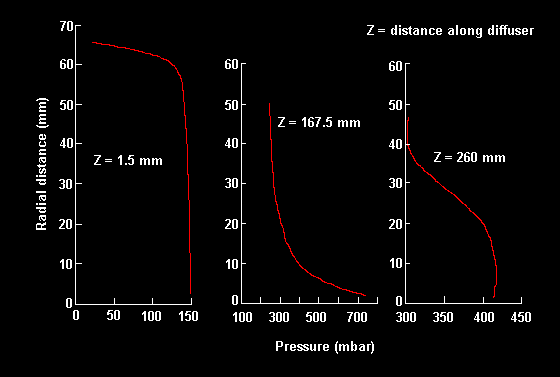
図３．半径方向圧力のプロファイル（計算値）

図４．ディフューザ入口での速度ベクトル図

考察：

・ディフューザ入口の円錐部や喉部における圧力は実験の結果と良く整合している

・これは、このような領域での流れや熱分布の予測にPHOENICSが適用できることを示している

・同様な形状、境界条件でスケールアップした計算は境界層厚さ以外において、同じ結果が得られるであろう

※実験とPHOENICSの計算の詳細は下記の論文を参照

Flow computation for high altitude test facility
A Leitner Heat and mass transfer group, RAFAEL, Haifa, Israel

高々度テスト設備のための流れ計算