| 目的: |
- PHOENICSで、偏心環状空間での非ニュートン流体の粘性流れを計算した
- 主な目的は、解析値や実験値とHerschel-Bulkley(HB)の流動モデルを用いた
PHOENICSの結果を比較することでPHOENICSの有効性を示すことである
|
|
| 概要: |
- この問題はドリルで穴を空ける時のドリルラインと岩石の間の環状空間内の
実際の流れと関連しています。さらに正常な穿孔中にでもドリルラインは穴の
中心にはないことが知られています
- 従って数値解析による予測は掘削技師にとって、特別な孔形状の場合に使用
する流体の流動性や流量を決定するための助けとなります。その結果、掘削、
輸送は効率よく行なえ、一方、環状の圧力が割れ目の下に残る
|
|
| 要点: |
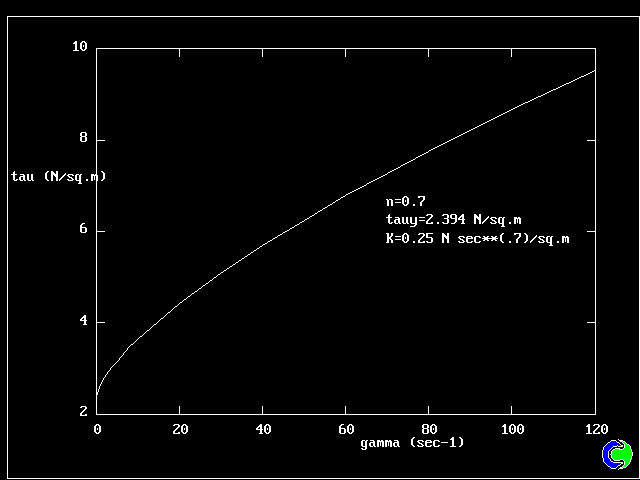
- HBモデルは、せん断応力τを、調和係数Kと降伏応力τy、べき乗指数nに
よって歪み率γとを関連付ける。即ち、 τ= τy + K*(γ**n)
- HBモデルはτyが0のときのべき乗モデルを単純化します。例えば、値が n<1
ならば、流動は擬似塑性(せん断流動化)であり、n>1ならば、ダイラタント
(せん断粘稠化)である。
- 降伏応力を越えたときに流動が始まります。
- n=1の時、HBモデルはBingham plasitcモデルになります。
- τy=0、n=1の時、ニュートン流体になる。
- 速度プロファイル、摩擦抵抗、圧力損失を計算するために、べき乗流体とHB
流体両方の完全に発達した層流流れとして単一平面ソルバーによって計算
されます。
- 無次元の形状パラメータを定義します:
偏心率 e = δ/ (Rin−Rout) (同心円の場合は0、1の場合は完全偏心)
ここでδは2つの中心間の距離、Rinは内側円の半径、Routは外側円の半径
になる。
|
| |
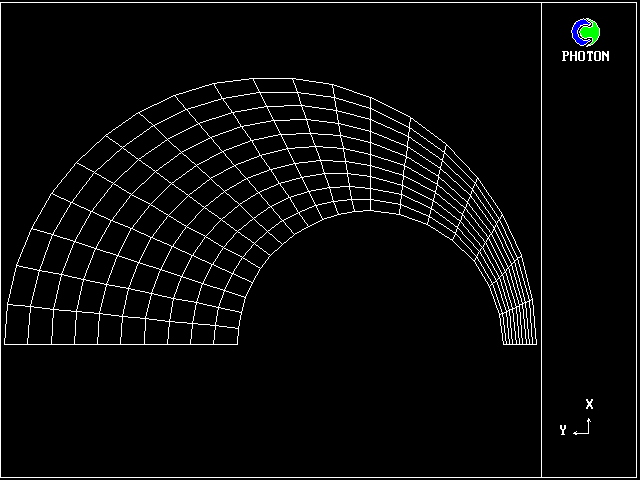
形状図はBFC座標系で、図2に示す。 |
|
| 1. HERSCHEL-BULKLEY FLUID:流量曲線 |
|
|
|
| 2. 偏心円形状図 |
|
|
| ・まず始めに、偏心円でのべき乗則流体の流れでPHOENICSの有効性を評価する。この
ケースの場合、Haciislamoglu とLanglinais [1] は圧力降下用の相関性を開発しました: |
| (dP/dZ)ecc=(dP/dZ)conc * R |
|
- (dP/dZ)conc は、同心円流れの圧力降下であり、有効径[2]を使い、Reedによって関連
付けられ計算されることができる。
- Rは、偏心率が0から0.95、パイプの直径比が0.3から0.9、べき乗指数が0.4から1の場合
に有効な下記の方程式により与えられる。
|
| R= 1 - .0072(r**.8454)(e/n) -1.5(r**.1852)(e*e)(n**.5) + .96(e**3)(n**.5)(r**.2527) |
|
| ここで、 |
| r = Din/Dout |
|
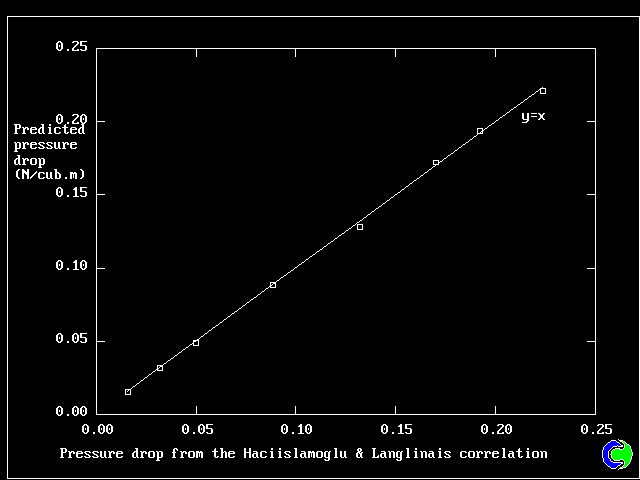
| この相関性の精度は、±5%以内である。PHOENICSが予測した圧力降下は、このパラ
メータの有効範囲内で相関性と比較された。その差異は、同じ精度の範囲内である。 |
|
|
| 3. 動力降下流動 : |
| 次のステップは、偏心円でのHerschel-Bulkley流体の流れをPHOENICSで評価する。相関性
は存在しない。従って計算の結果はHaciislamoglu と Langlinaisの結果[1]によって評価する |
|
| 流体の物性を以下に示す : |
|
| _ n = .7 |
| _ K = .25 kg/ (m sec**n) |
| _ tauy = 2.394 N/m**2 |
| _ flow rate Q = 1.2618e-2 m**3/sec |
| _ Din = 25.4 cm |
| _ Dout = 12.7 cm |
|
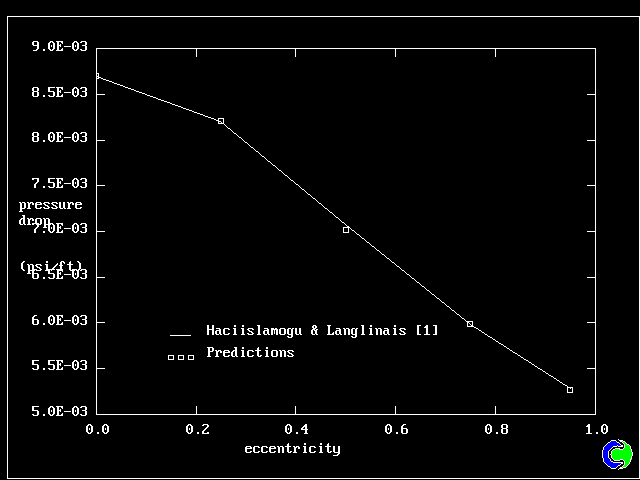
| 我々はまずPHOENICSの圧力降下を比較する。この影響はよく知られていることに気づくだ
ろう。一定流量の流れでは、摩擦による圧力損失は偏心率が増すにつれて減少している。
この結果は、HaccislamogluとLanglinais の圧力損失と良く一致している。 |
|
| 計算 VS 相関 |
|
|
|
| 4. HERSCHEL-BULKLEY 流動 : |
| 圧力降下 vs 偏心率 |
|
|
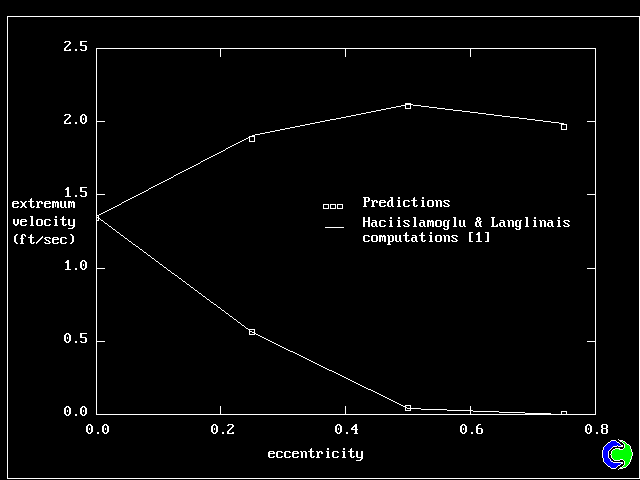
| それから、2つの速度の極値を比べることによって速度のプロフィールをチェックする。2つの極値
とは、環状部の最も広い箇所と最も狭い箇所の最大速度である。その結果は、Haccislamoglu と
Langlinaisの結果と良い一致が得られている。(fig.5) |
|
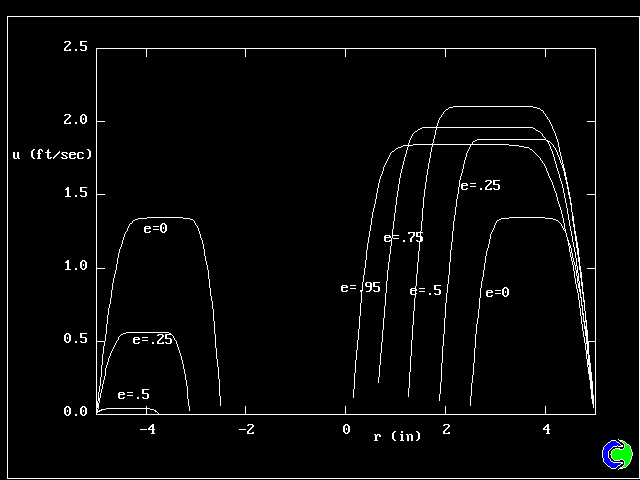
| 我々は偏心率が増したときの影響を知ることができる。: 流体が広くなっている部分に集まると
環状部の狭いところでの速度は減少する。(fig.6) 偏心率が高い(5以上)時は、環状の拡大部で
速度が大きい箇所(平坦な速度分布)があり、一方で、狭い部分では流れ場がないところもある。 |
|
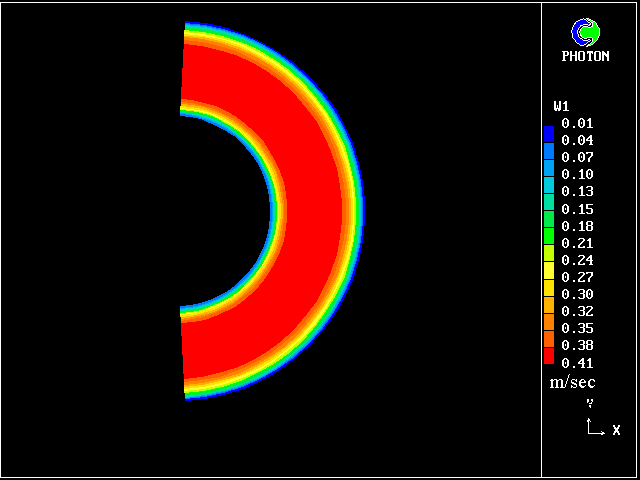
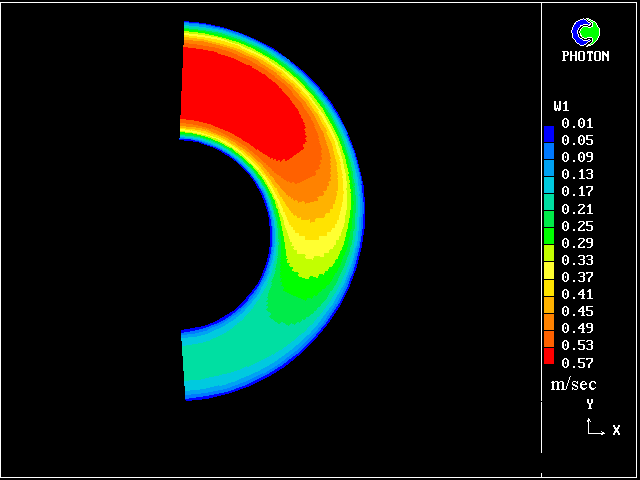
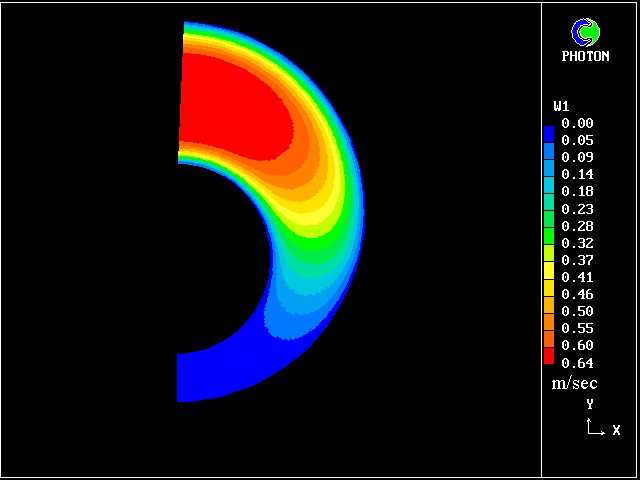
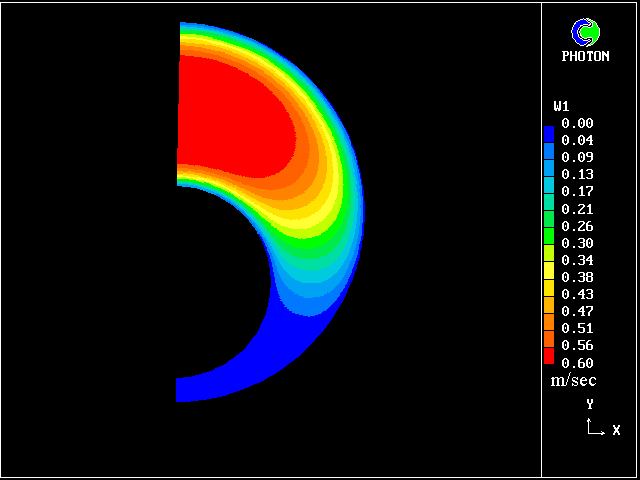
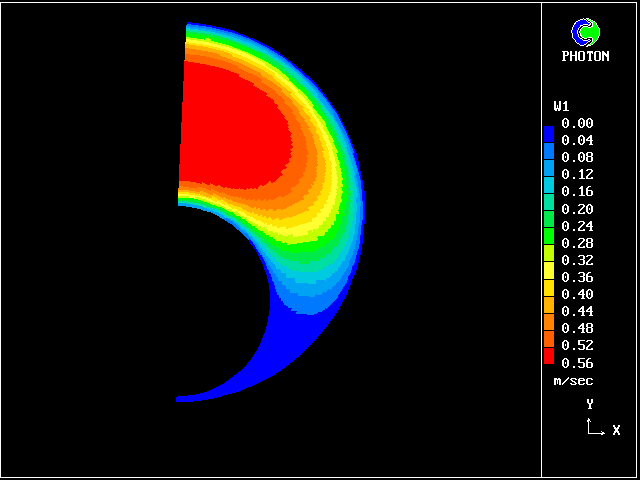
| 偏心率の違いにより遅い速度場が生じる。 (fig. 7,8,9,10,11) |
|
|
| 5. HERSCHEL-BULKLEY FLUID : 極値 ve 偏心率 |
|
|
|
| 6. HERSCHEL-BULKLEY FLUID : 半径 ve 速度分布 |
|
|
|
| 7. HERSCHEL-BULKLEY FLUID : 速度分布 (E=0) |
|
|
|
| 8. HERSCHEL-BULKLEY FLUID : 速度分布 (E=.25) |
|
|
|
| 9. HERSCHEL-BULKLEY FLUID : 速度分布 (E=.50) |
|
|
|
| 10. HERSCHEL-BULKLEY FLUID : 速度分布 (E=.75) |
|
|
|
| 11. HERSCHEL-BULKLEY FLUID : 速度分布 (E=.95) |
|
|
|
| 参照文献: |
|
| [1] M. Haciislamoglu, J. Langlinais, 1990, "Non-Newtonian flow in eccentric annuli", Journal of Energy Ressources pp 163,169 |
|
[2] T.D. Reed, Conoco Inc, A.A. Pilehvari, U. of Tulsa, 1993, "A new model for laminar, transitionnal, and turbulent flow of Drilling muds", Society of Petroleum Engineers, SPE 25456, pp 39, 52 |
|
|