Dr. R. P. Hornby email:bob.hornby007@gmail.com
はじめに
海洋の表層付近は風による乱流によって混合されるため、通常密度は均一ですが、海洋深部では密度成層されています。表面混合層の深さは一般に風の強さと持続時間に依存しますが、1 メートルから数百メートルまで変化します。海洋の密度成層深部で膨張収縮または屈曲する物体 (魚、潜水艇など) は、物体から離れて伝播する内部波を生成し、いくつかの異常な特性を持ちます。特に、膨張収縮する物体からの内部波は、一定の波位相の線に垂直ではなく、それに沿ってエネルギーを伝播します。これらの特性については、参考文献 1 で詳しく説明されています。この記事では、PHOENICS を使用してこれらの特性のいくつかを説明しますが、移動体に対する MOFOR 機能を使用して計算を拡張します。
解析方法
PHOENICS は、一様に成層した環境で運動体が曲がるときに、質量運動量とエネルギーの 2 次元および 3 次元の時間依存層流方程式を解くために使用されます。直交座標グリッドは Koren 差分スキームで使用されます。局所浮力周波数は次のように与えられます。
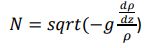
ここで、g は重力加速度、ρ は密度、z は垂直座標です。
検討する最初の2次元ケース(ケース1)は、静止した物体で、振動数ωがN未満に設定された、物体全体の垂直正弦波振動(速度wb)の場合です。
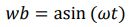
ここで、a は振幅、t は時間です。より複雑な状況は、特定の周波数における体内の細胞の局所速度を適用することで分析できます。たとえば、体内の細胞の正弦波速度が次の式で表されるケースが考えられます (ケース 2)
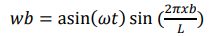
ここで、xb は体の側面座標、L は体の長さです。
シーソーのような物体の速度も分析できます(例3)
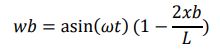
さらに興味深いケースとして、全身の速度の短時間の突然の変化を検討することができます(ケース4)
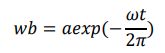
このタイプの解析は、物体が並進運動と屈曲運動の両方を行う 3D 過渡ケースに拡張できます。この場合、屈曲による振動波は、並進運動から生じるかなり異なる波に重ね合わされることが予想されます。
計算結果
周波数ωがNより小さい波はΘ方向に見られることが示されています(文献1)。ここで
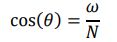
ケース1ではωはN/sqrt(2)に設定されているため、内部波エネルギーは垂直に対して45度で伝播すると予想されます。PHOENICSの結果は図1に示されており、同じ周波数のシュリーレン実験結果(密度勾配の測定)と比較されています。波エネルギーの伝播方向については非常によく一致しています。
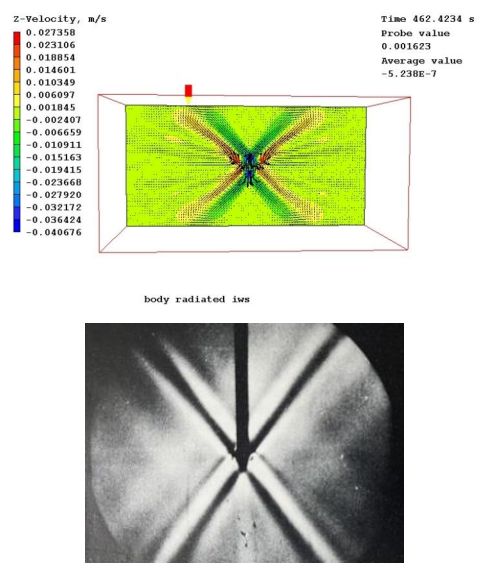
図1 上の図は、均一に成層した流体内で周波数N/sqrt(2)で垂直方向に振動する中心物体のPHOENICS速度ベクトルと垂直方向の速度等高線を示しています。下は同等の実験結果です(Ref 1 p314、図76より引用、写真はD. H. Mowbrayによる)
ケース 2 と 3 では、特定の周波数で物体内部に反対方向の動きが伴い、物体全体の位相変化と動きの水平方向の変位により、より複雑な図が生成されます。これは、ケース 2 の速度を使用して図 2 に示されています。ケース 3 の速度を使用しても同様の結果が得られています。
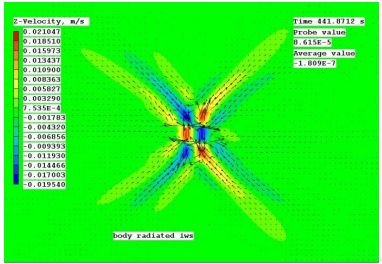
図2. 均一成層流体内で周波数N/sqrt(2)で垂直方向に振動する中心物体のPHOENICS速度ベクトルと垂直速度の等高線。変位と位相の影響を示すために垂直速度の等高線が示されています(ケース2)
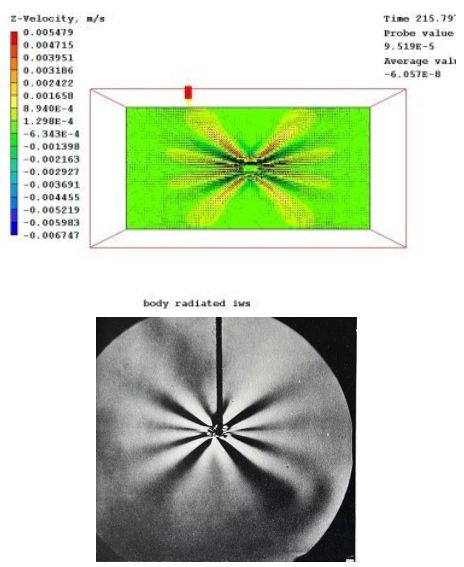
図 3. 上の図は、物体の短時間の変位に対する PHOENICS の初期結果を示しています (ケース 4)。下の図は、同様の設定での初期の実験結果を示しています (Ref 1 p315、図 77a より引用、T.N. Stevenson 撮影)
ケース 4 では、体全体の変位が突然短時間変化し、さまざまな波長と周波数が生成されます。図 3 と 4 は、外乱の開始から 2 時点の波形パターンの PHOENICS と実験結果 (同様の設定) を示しています。
図 3 は、擾乱の発生から早い時点の結果を示し、図 4 は、その後の時点の結果を示しています。これらの図は、擾乱の異なる周波数成分によって複数の波線が発達していること、および、一定時間内に長い波長が遠くまで伝わるにつれて、発生源に向けられた角度が時間とともに減少していることを示しています。いずれの場合も、PHOENICS の結果は実験の結果を非常によく表しています。
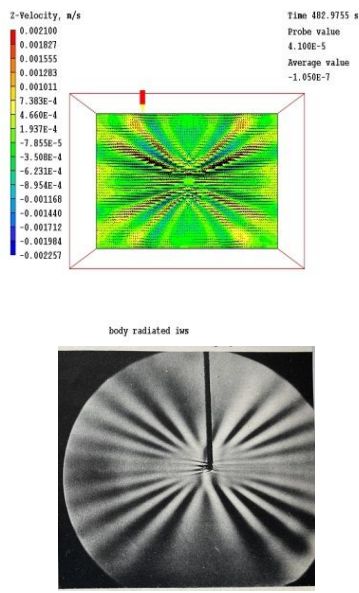
図 4. 上の図は、物体の短時間の変位に対する PHOENICS の後の時間結果を示しています (ケース 4)。下の図は、同様の設定に対する後時間の実験結果を示しています (Ref 1 p315、図 77b より引用、T.N. Stevenson 撮影)
まとめ
PHOENICS の結果は、成層流体内の物体の 2D 垂直振動について示されています。剛体の振動の結果は、同等の実験とよく一致することが示されています。さらに、MOFOR 技術の使用により、物体の屈曲の調査に拡張することができ、この技術を適用した 2D の結果がいくつか示されています。この方法は、移動と屈曲の両方を行う物体を調査するために 3D にさらに拡張することができ、これについては今後の記事で概説する予定です。
参考文献
1. Li??ghthill M J. Waves in Fluids、Cambridge University Press1978
2. Hornby R P. PHOENICS Modelling of a Moving Body in a Stratified Tank. PHOENICS Newsletter Winter 2019。
|