1. THINC/WLIC
以前の PHOENICS ニュースレター [1] では、PHOENICS 2018 バージョン 1 の Volume-Of-Fluid (VOF) 機能に、混ざり合わない流体や自由表面流れの高解像度界面キャプチャ スキームがどのように追加されたかについて説明されていました。
また、それには界面での表面張力効果をモデル化する機能も備えています。この記事では、2018後半にリリースが予定されている PHOENICS 2018 バージョン 2 で使用するための自由表面機能の追加の開発について報告します。このアップグレードには、THINC/WLIC [2-3] 界面キャプチャ スキーム、および界面と固体壁の間の接触角、ならびに表面張力の温度依存性を説明する強化された表面張力モデルが含まれます。
双曲線正接関数を使用して、THINC (界面キャプチャ用双曲線正接) スキームと呼ばれる健固で振動と滲みのないスキームを追加されました。また、このスキームは、幾何学的な再構成を行わない既存のほとんどの方法と比較して、競争力のある精度を示しています。WLIC (重み付きラインインターフェース計算) メソッドは、表面法線から計算された重みを使用して、各座標方向に沿ってラインインターフェースの平均を取得することにより、THINC スキームを多次元に拡張します [3]。
双曲線正接は、それ自体が階段状のジャンプ分布特性を持つ最も単純な連続関数です。THINC スキームは、区分的に変更された双曲線正接関数を使用します。
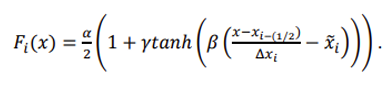
パラメータ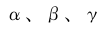 は、数値解の品質を決定するために重要です。 は、数値解の品質を決定するために重要です。
元々の THINC-WLIC 法は完全に陽的ですが、PHOENICS の SIMPLEST アルゴリズムでは、必要に応じて陰解法と保守的な形式のマーカー変数を使用しています。
THINC-WLIC 法は、自由表面流の古典的なベンチマーク、つまり速度が時間と空間に依存する Rider-Khote [4] 逆渦でテストされました。半径 0.15 の円は、最初は (0.5, 0, 75) を中心とし、次に THINC/SW (傾斜重み付け [2]) スキームによって 0 から T/2 時計回りに、T/2 から T=8 まで反時計回りに転送されます。T/2、T、およびその他の中間時間での数値結果を以下の図 1 に示します。
界面は T/2 でらせんに変形されており、他のすべての既存の VOF スキームとまったく同じように、細い尾が小さな液滴に分割されていることを除いて、十分に解決されています。
2. 表面張力モデル: キャピラリー項とマランゴニ項
PHOENICS では、表面張力効果は Brackbill の連続体表面力 (CSF) モデルによって表されます [5]。このモデルは、マーカー変数φの遷移領域によって定義されるように、界面の近くでのみ作用し、連続体の体積力は次から計算されます。
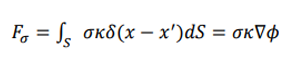
ここで、φは体積分率、xは位置、x’は界面の位置、σは一定の表面張力係数、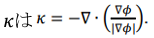 で与えられる界面の曲率です。 で与えられる界面の曲率です。
勾配▽φ は、境界にまたがる 2 つの値から直接評価されます。 σが定数の場合、表面張力は次の式で表すことができます。
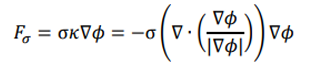
自由表面の平均曲率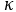 は以下で与えられます。 は以下で与えられます。
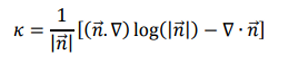
ここで、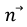 = ▽Φ は法線です。この定式化により、有限差分を使用して勾配を計算する際の精度が向上しますが、ここで、高さ関数 [6-7] や CLSVOF (結合されたlevel-set VOF) [8]、 = ▽Φ は法線です。この定式化により、有限差分を使用して勾配を計算する際の精度が向上しますが、ここで、高さ関数 [6-7] や CLSVOF (結合されたlevel-set VOF) [8]、 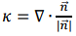 により直接計算できます。これらのアプローチは PHOENICS のオプションとして実装されていますが、有限差分を使用して法線を計算するほど正確ではありません。 PHOENICS で導入された方法は、 により直接計算できます。これらのアプローチは PHOENICS のオプションとして実装されていますが、有限差分を使用して法線を計算するほど正確ではありません。 PHOENICS で導入された方法は、 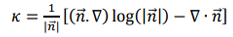 として曲率を計算することです。さまざまなテストケースやアプリケーションに対して、これらのさまざまなアプローチを評価および比較する必要があります。 として曲率を計算することです。さまざまなテストケースやアプリケーションに対して、これらのさまざまなアプローチを評価および比較する必要があります。
表面張力が可変で、温度や濃度に依存する場合 (いわゆるマランゴニ効果)、表面張力には運動量方程式に追加の項があります。
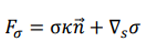
ここで、表面勾配は次のように定式化されます。
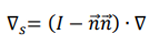
ここで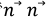 という表記は、ベクトルの外積に使用されます。例えば という表記は、ベクトルの外積に使用されます。例えば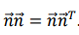 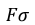 に対する上記の式の右辺の項は、それぞれキャピラリー力とマランゴニ力として識別できます [9]。 に対する上記の式の右辺の項は、それぞれキャピラリー力とマランゴニ力として識別できます [9]。
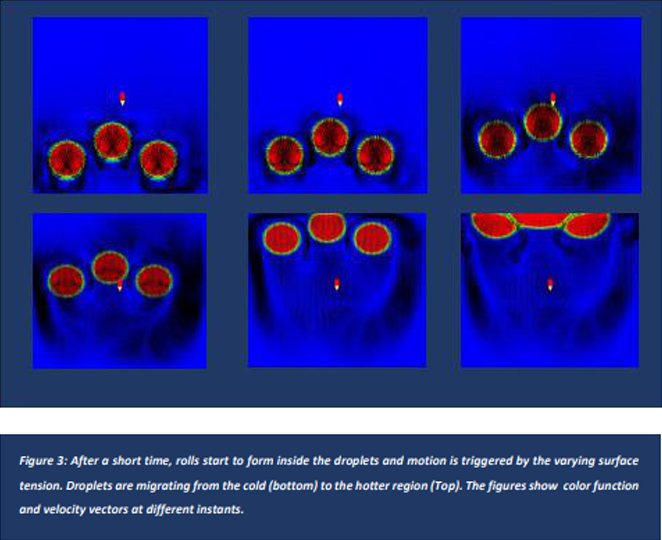
次の 2 次元の例では、無重力条件下での空気で満たされた空洞内の 3 つの水滴の熱毛管移動を考慮しています。 PHOENICS は、熱マランゴニ効果により、変化する温度場で液滴がどのように移動するかを予測するために使用されます。
流体が最初は静止しており、表面張力は温度に従い変化し、キャビティの底面と上面はそれぞれ 20°C と 50°C に維持され、初期温度場は次第に変化します。液滴の移動は、温度勾配によって駆動されます。温度勾配は、冷たい領域から熱い領域への流れを駆動する表面張力勾配をもたらします。
参考文献
1. J.Ouazzani & J.C.Ludwig, "Development of Interface Simulation Methods in PHOENICS", PHOENICS Newsletter, Autumn, CHAM Limited, Wimbledon, London, UK (2017).
2. F.Xiao, S.Li & C.Chen, “Revisit to the THINC scheme: A simple algebraic VOF algorithm”, J.Comp. Physics 230, 7086? 7092, (2011).
3. K. Yokoi, “Efficient implementation of THINC scheme: a simple and practical smoothed VOF algorithm”, J. Comp. Physics. 226, 1985?2002, (2007).
4. W.J.Rider & D.B.Kothe, “Stretching and tearing interface tracking methods”. AIAA paper, 95, 1?11, (1995).
5. J.U. Brackbill, D.B. Kothe and C. Zemach, “A continuum method for modelling surface tension”, J. Comp. Physics, Vol. 100, p. 335, (1992).
6. B.D. Nichols, C.W. Hirt, R.S. Hotchkiss, “SOLA-VOF: A solution algorithm for transient fluid flow with multiple free boundaries”, Technical Report LA8355, Los Alamos National Laboratory, (1980).
7. J. Helmsen, P. Colella, “Non-convex profile evolution in two dimensions using volume of fluids”, Technical Report UCRL-ID-126402, Lawrence Livermore National Laboratory, (1997).
8. M. Sussman, “A second order coupled level set and volume-of-fluid method for computing growth and collapse of vapor bubbles”, J. Comp. Physics 187, 110?136, (2003).
9. H.V. Patel, S. Das, J.A.M. Kuipers, J.T. Padding, E.A.J.F. Peters, “A coupled Volume of Fluid and Immersed Boundary Method for simulating 3D multiphase flows with contact line dynamics in complex geometries”, Chemical Engineering Science 166, 2841, (2017)
|