はじめに
水中爆発の影響に関する知識は、軍事用途でも民間用途でも重要です。 通常、水中爆発は、高温高圧のガスを生成する急速な化学反応で始まります。 この膨張する気泡は衝撃波を発生させ、高速で水中に進みます。 気泡圧力は膨張するにつれて周囲圧力を超えて減少し、その時点で気泡圧力は収縮して、連続的に小さな気泡圧力パルスを生成します。 このプロセスのあらゆる側面をモデル化することは、ガスと水の境界面の移動が関与するため非常に複雑です。 しかし、衝撃波伝播の重要なプロセスは、より単純であり、この側面が本テーマの基礎になります。
モデリングの基礎
水中の衝撃伝播をモデル化するには、水の密度を圧力、温度、塩分に関連付ける状態方程式が必要です。(1) 圧力 p のみの関数として密度のより的確な関係は、Taitの式 (2) と呼ばれます。
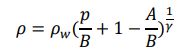
ここで、基準密度 RHOM は 1000 kg/m3、A、B の値はそれぞれ 105 Pa と 3.31x108 Pa、GAMMA=7.15 です。 どちらの関係も音速 c を与えます。
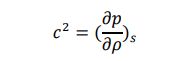
通常、水中の音速は周囲条件下では約 1500m/s ですが、水中爆発で遭遇する非常に高い圧力ではさらに大きな値に増加します。
衝撃波の狭い領域全体に質量と運動量の保存を適用すると、圧力と密度から衝撃速度 U m/s が得られます (3)。
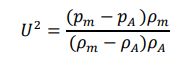
ここで、添え字A は衝撃前の周囲条件を表し、添え字m は衝撃のすぐ下流の状況を表します。衝撃後の流速umは以下の式としても求められます。
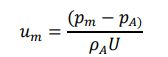
特に、衝撃波を横切る圧力ジャンプの範囲を指定することにより、上記の関係を使用して衝撃 U と流量 μm 速度を pm の関数として決定できます。これらの結果を参考文献 4 の結果と比較することでチェックできます。Fofonoff の式を使用した場合を図 1に示します。ここで非常に良好な一致を示しています(Tait 式でも同様の結果が得られます)。
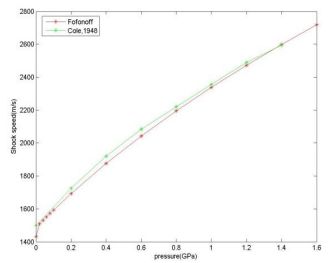
図 1−1: 計算された衝撃波速度
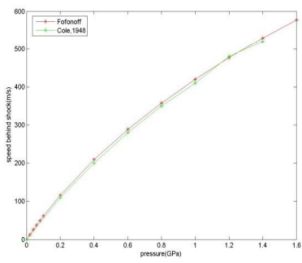
図 1−2: 計算された流体速度
PHOENICSでのモデル化
図2−1に示す最も単純なケースでPHOENICSで計算しました。初期条件として長さ 200 m のチューブの左側の高圧水 (4x108 Pa)と右側の低圧水 (105 Pa) に分離しておきます。また両側とも初期水温は同じ14℃であると仮定しました。この初期状態から非定常計算を開始します。これにより、衝撃波が右に進み、膨張波が左に進む典型的なショックチューブの流れが生じます。これは、PHOENICS によって 時間依存性を持つ1次元圧縮性流れとして計算されます。ここで、PHOENICSは圧力の関数として定義される密度とともに質量運動量とエネルギーの保存方程式を解きます。
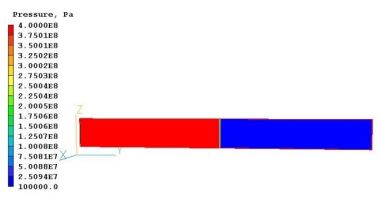
図 2−1: シミュレーションの初期設定 左:高圧水 (赤)、右:低圧水 (青)
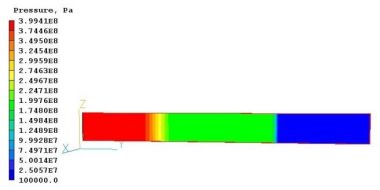
図 2−2: 計算開始から少し経った圧力分布
計算開始から少し経った後のシミュレーションの結果が図2−2に示します。圧力コンターで右に進む衝撃波と左に進む膨張波がはっきりと確認できます。
図3は、シミュレーション中の各時刻の圧力分布を示しています。これらのプロットから、衝撃速度と膨張波 (局所音速で伝わる) の速度を計算できます。これらの値は、上記の方程式から計算された値と比較できます。図 4 は、FofonoffとTaitの両方の密度関係式について非常に良好であることを示しています。
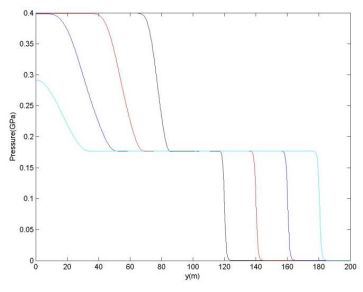
図 3: 同じ時間間隔の圧力プロット
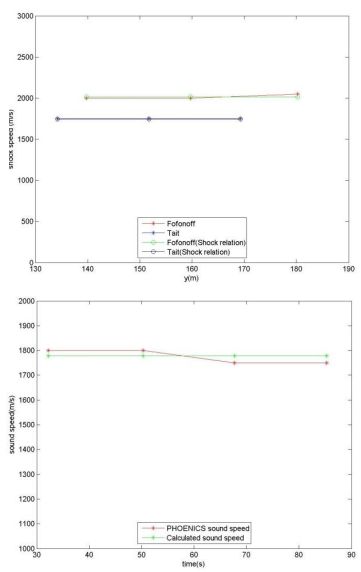
図 4: 衝撃波(上)と膨張波(下)の速度とPHOENICSから計算された速度の比較
海中での実験で最も一般的な爆発物は、主に TNT で構成される 0.82kg SUS (Signal Underwater Sound) 火薬です。海洋試験に基づく経験的な関係は、装填重量w(kg)、および射程 R(m) の関数であらわされるピーク衝撃圧力 pm について Chapman によって示されています (5)。
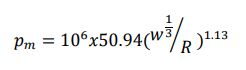
衝撃通過後の圧力の指数関数的減衰は次の式で与えられます。
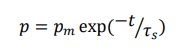
ここで、時定数は次のように与えられます。
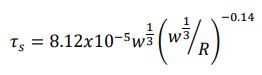
これらの関係が気泡と衝撃波の形成について初期段階で維持されると仮定すると、圧力の時間変化を関して 固定したPHOENICSのセルで、爆薬の簡素化されたシミュレーションを可能にすることができます。半径 10m の領域の中心に 0.82kg の SUS 装薬を配置した軸対称シミュレーション結果を図 5 に示します。t=0.003 秒での衝撃速度 (図 5 上) は、圧力により約 1700 ms-1 です。中心からの距離に反比例して減少します。等間隔の時間間隔での圧力プロットが、図の下部セクションに表示されます。
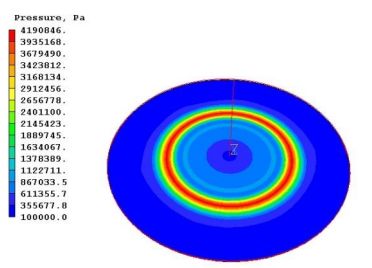
図 5: 爆薬の爆発後の衝撃波を示す圧力コンター図
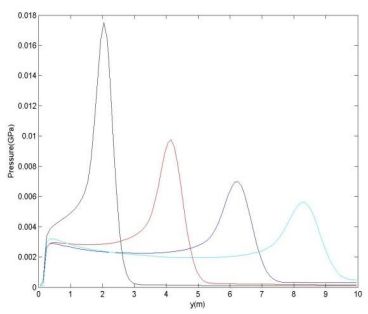
図 6: 同じ時間間隔の圧力プロット
結論
上記の結果は、水の密度と圧力を関連付ける Fofonoff 式または Tait 式のいずれかが、水中での衝撃波の伝播、またはより一般的には水中での音の伝播をシミュレートする際に PHOENICS でうまく機能することを示しています。
参考文献
1. Fofonoff N P, Physical Properties of Seawater: A New Salinity Scale and Equation of State for Seawater,
J Geophys Res vol 90, p3332 (1985).
2. Li Y H, Equation of state of water and seawater,
J Geophys Res 72, 2665-2678 (1967).
3. Medwin H, Clay C S, Fundamentals of Acoustical Oceanography,
Academic Press (1998).
4. Cole R H, Underwater Explosions,
Princeton University Press, Princeton, N J, (1948).
5. Chapman N R, Measurement of the waveform parameters of shallow explosive charges,
The Journal of the Acoustical Society of America, 78, 672 (1985).
|