1.はじめに
群集がどのように振る舞いをするかを予測することができることは安全を守る上で重要である。
例えば宗教的な祭りに参加する人々の安全、スポーツイベント、音楽祭り、全国的なお祝い、デモンストレーションや空港での人々の動き、駅や客船などでの人々の動きなどである。
一例として、Hajj に関連した多くの群衆の墜落事故が過去に発生している。Hajj は、メッカで毎年行われる巡礼であり、体力および経済的に余裕があれば、少なくとも一回はイスラム教徒が生涯遂行する義務として定められている。
2015 年 9 月 24 日、巡礼者がメッカ近くのサウジアラビアの Mina の歩行者用の橋 Jamaraat Bridge に向かう途中で、2000 人以上の死亡が報告されている(Fig.1)。

Fig. 1: Crowds of pilgrims making their way to the Jamaraat Bridge (2011)
群衆行動をモデル化するには2つの基本的な方法がある(参考文献1)。
1番目のアプローチは、群衆を特定の規則に従う個々の実体(entities)で構成されているとみなし、これらの集合体で群衆の行動を決定する。
これはMonte-Carloアプローチに似ており、多数の実体が関与する場合には予測コストが高くなる。
2番目のアプローチは、群衆を質量と運動量の保存に従った2次元連続体としてモデル化することです。
後者のアプローチは計算流体力学に特に適しており、このような問題でPHOENICSどのように使われるかは興味深いことである。
以下、PHOENICSを用いた群集行動のモデリングをついて説明する。
2.PHOENICSによるモデリング
モデリングの練習として、50m×50mのエリアで最大2つの出口点を持つ群衆の行動を考える(必要に応じて追加可能)。
まず、高い集団密度を領域の中心に設置し、変化する密度分布および群衆の流れについて単一の出口を介して調べる。
次に、2つ以上の出口および閉塞の影響を伴うより複雑な状況を考慮する。
標準的なPHOENICS質量および運動量方程式による群集の動機および方向効果をモデル化するために、運動量方程式に含まれる密度(圧縮性流れ)およびソース項に関連する圧力が使用される。
詳細は以下の通りである。
圧力(p)、密度(ρ)の関係は、
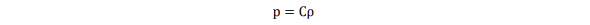
Cは定数で、O(1)(参考文献1)である。これはシグナル伝達速度を意味する(圧力はC1/2に比例する支配的な力を提供)。
運動量方程式のソース項は、個人の原動力と「抗力」(速度に比例すると仮定)を表す。
これらの力は、最も近い出口または最も近い目に見える出口に向かっていると仮定する。
密度が低い場合、原動力が支配的であると予想されるが、密度が大きい場合は圧力が支配的になるので、原動力は密度で直線的に補間される。
ボリュームソース項は次のようになる。
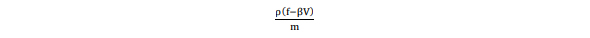
ここで、ベクトルfは補間された原動力であり、Vは速度ベクトルであり、両方とも最も近い出口または最も近い目に見える出口に向けられる。
βは定数であり、mは平均人体質量である。
最大速度Vmaxは、密度が最も低い領域に現れ、定数m/βで与えられる。
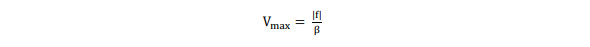
ドメインを、xおよびy座標方向に50個のセルを有するデカルト格子を使用して離散化する。
KORENスキームをCourant条件を満たすように使う。
ローカライズされた(xc、yc)の群衆密度は次のようになる。
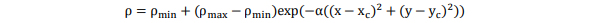
ここで、ρ_maxは最大(局在化された)密度、ρ_minは最小(背景)の密度とαは群衆の大きさを決める定数である。
境界条件として、密度が大きいときに重要となるフリースリップ条件を導入。
出口ポイントでは、圧力固定(0.1Pa)にする。
これは出口の形状や窒息の可能性も考慮できるより現実的な設定である。
Cは1、mは100kg、Vmaxは2.5m/s、原動力は100N、ρ_maxは200kg/m^3(例えば密度が高い場所では4人/m^2)とする。
ρ_minは0.1kg/m^3とする。これらは合理的だと思われる。
3.結果
最初に取り上げるケースでは、ドメインの中心に局所的な群衆分布があり、右上隅(a,b)が出口である。
aとbはそれぞれx方向とy方向ドメインサイズである。
人々の避難を必要とする外乱が発生することを想定する。

Fig.2 Crowd density and velocity vectors after 0.1s(top) and 8s(bottom). Exit is situated at the top right hand corner.
結果をFig.2に示す。群衆の動きはほぼ直ちに出口に向かい、対角線の周りに対称的に分布して時間とともに移動する。
低密度領域における速度の大きさも、最大予測速度Vmaxに密接に対応している。
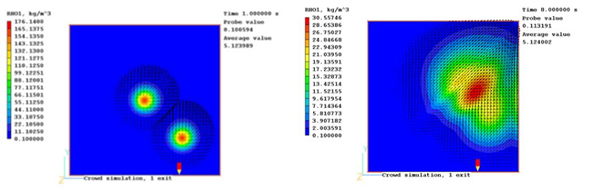
Fig.3 Crowd density and velocity vectors after 0.1s (top) and 8s (bottom). Exit is situated at the topright hand corner.
Fig.3は2つのローカライズされた群衆密度分布を示す。結果から見ると、出口に向かって2つの局所的な群衆が合流する。この場合、対角線より下のより大きな「流れ」が確認できる。
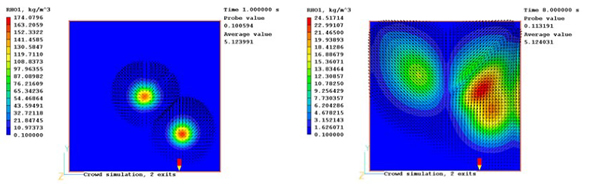
Fig. 4. Crowd density and velocity vectors after 1 s (top) and 8 s (bottom). There are two exits at the top left and top right hand corners.
Fig.4は、2つの局所的群衆分布と2つの出口(ドメインの左上と右上)でより興味深いケースを示している。
実際に予想されるように個人の動機は最も近い出口に向けられており、図から分かるように右上の出口に向かって顕著な偏りを示す結果となった。
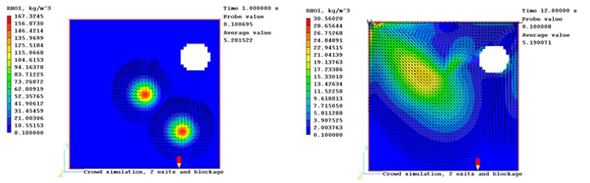
Fig5. Crown density and velocity vectors after 0.1 s (top) and 8 s (bottom). There are two exits at the top left and top right hand corners and a circular blockage near the top right exit.
Fig.5は、2つのローカライズされた群衆分布、2つの出口、および円形閉塞を伴う結果を示す。
閉塞は流れを妨げ、右上の出口を不明瞭にする傾向が現れる。
結果的に、人々が最も近い出口に向かって移動する傾向がモデリングに含まれたが、右上の出口が見えないため、多くの群衆が左上の出口に向かっている。
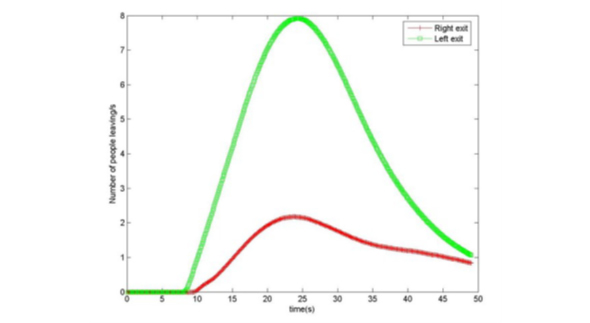
Fig6. Number of people leaving the domain per second through each of the two exits when there is a circular blockage near the top right exit.
Fig.6は、時間の関数として各出口を通過する人々の割合を示した。
人々が出口に到達するまでには有限の時間がかかりますが、左手出口は常に約25秒後にピークとなるより大きな流出を形成することが分かる。
4.まとめ
かなりシンプルで物理的に動機付けされたモデリングの追加によって、PHOENICSは群衆の行動に対して妥当な計算結果を出していることを示した。
計算は、各時間ステップでうまく収束した。
2次元計算であるため、マシンに対する要求も低い。
しかし、出口率を制限する可能性のある出口の幾何学的形状については、さらに考慮する余地がある。
実際の群衆運動の結果との比較やそれに続くモデリングの洗練が必要であり、群衆の行動で死者を出す可能性のあるようなより複雑なシナリオ(Fig.1)を考慮することで用途が広がると思われる。
|