PHOENICS は、有限体積法をもちいて質量、運動量、エネルギー等の保存式を、定常または非定常計算で空間1次元〜3次元を反復法を使用して解く汎用熱流体解析ソフトウエアです。
| 空間離散化 |
有限体積法(コントロールボリューム法) |
| 時間依存性 |
非定常計算・・・完全陰解法、陽解法
定常計算・・・擬似時間法 |
| 圧力速度結合 |
Simplest法 |
| 線形方程式反復法 |
ガウス法、slabe-wize法、whole-field法 |
【PHOENICSで用いる支配方程式】
流体の現象は、大きく以下の3つの保存則(つりあいの式)からなりたっています。
1)質量保存則連続の式
2)運動量保存則運動方程式
3)エネルギー保存則エネルギー保存式 |
これらが、ある空間内で時間的に満足するように連立方程式を組みたてて計算します。
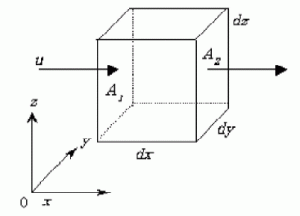
図1 コントロールボリュームにおける流束のつりあい
■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■
1.連続の式
流体中に、ある固定した領域(コントロールボリューム)を設定し、その領域に出入りする質量の総和がゼロであることから、質量保存則を定式化したものを連続の式といいます。
図1のように、直交直線座標系で速度ベクトルVの流れ場の中に置かれた微小な直方体のコントロール・ボリュームを考えます。それぞれの一辺はdx, dy, dzの長さをもつことにします。一般に流体の速度は場所と時間の関数であり、速度ベクトルV(x, y, z,t)のx, y, z軸方向成分は、それぞれu(x, y, z, t), v(x, y, z, t), w(x, y, z, t)と書けます。
ここでx軸に直交する面A1, A2における流入出質量について考えます。
A1から単位時間あたりに流入する質量mdotA1は流体の密度をρ(x, y, z, t)とすると
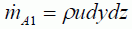
またA2から単位時間あたりに流出する質量mdotA2 は次のように表されます。
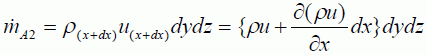
従って、単位時間あたりの質量増分は、x軸に垂直な面A1,A2間を通過してコントロールボリュームに流入出する流量から、方向ベクトルに注意して面を横切る流量の和をとり
(質量増分)=(流入質量)−(流出質量)
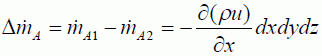
になります。同様にy,z軸に直交する面について単位時間あたりの質量の増えた量をあらわし、それらの総和から次式が得られます。
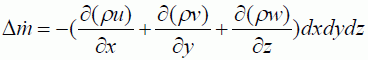
上式はコントロール・ボリュームの単位時間あたりの質量増分を表します。
一方、コントロール・ボリュームの質量は、密度と体積の積であることから、単位時間あたりの質量変化は次のようにも書けます。
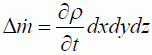
上の両式が等しいことから変形すると、次式が得られます。
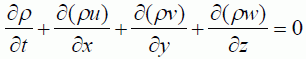 ・・・(3,1) ・・・(3,1)
これを連続の式といいます。さらに非圧縮流れでは、ρ=constですので次のようになります。
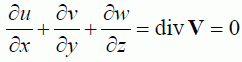 ・・・(3,2) ・・・(3,2)
連続の式の物理的考え方は、単位体積における質量の時間的増加量 Δρ /Δtと、面を横ぎる質量流束 ρV の空間的発散量 div(ρV) の和は0、つまり質量は増加も減少もしないということになります。
密度一定の場合(3,2)式、密度変化がある場合(3,1)式を考えます。また境界条件で明示的(流入、湧き出し、質量消滅、流出など)なソースは右辺の0の変わりにその量を右辺に与えることで表されます。
■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□
2.化学種の保存式
連続の式を用いて化学種i成分の場合を考えます。多成分の場合でも1つの成分に着目すれば、化学種iについて以下の質量保存が成り立ちます。
Ri は単位時間・単位体積当りの生成速度で、化学反応等による成分の変化量を表します。
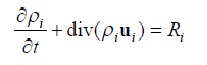 (2-1) (2-1)
ここで、Yi を化学種の質量分率、ρを混合密度とすると、ある体積中にふくまれるi 成分の質量はρi= ρYi になります。一般的な従属変数φの流束ベクトルをJとすると、
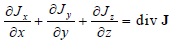 (2-1a) (2-1a)
であることから、平均速度場 u では次式が得られます。
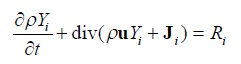 (2-2) (2-2)
(2-1)式と(2-2)式は全く同一です。 ここで、
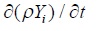 は、単位体積あたりの化学種の質量変化率を示しています。 u Yi の値は化学種の対流流束、すなわち一般的な流れ場ρuによって運ばれる流束のことです。J i は拡散流束を意味し、通常これはYi の勾配に依存します。ここで、拡散流束J i をフィックの法則を用いて表すと、 は、単位体積あたりの化学種の質量変化率を示しています。 u Yi の値は化学種の対流流束、すなわち一般的な流れ場ρuによって運ばれる流束のことです。J i は拡散流束を意味し、通常これはYi の勾配に依存します。ここで、拡散流束J i をフィックの法則を用いて表すと、
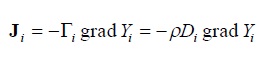 (2-3) (2-3)
Di は拡散係数です。 拡散係数とは成分による速度差(スリップ速度)の効果をあらわす指標を意味しています。(2-3)式を(2-2)式に代入すると、化学種の保存式が得られます。 Sc はシュミット数、v は動粘性係数です。
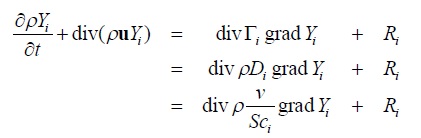 (2-4) (2-4)
【成分質量保存の追加の情報】
(1)上記のように成分の質量保存について質量分率を解くので、混合密度とセルの体積をかけると、その場所にある質量が得られます。
混合密度というものが大きな意味をもつことに注意してください。
(2)n成分の質量分率の総和は1なので、n成分1つの成分は、
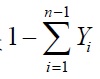 からもとめることができます。 からもとめることができます。
(3)質量分率は保存される量です。しかし工学的に濃度は、体積を基準にすることがしばしばあります。単位は
[m3_i/m3]、[mol_i/mol]、[mol_i/m3]です。もし成分の密度(分子量)がほとんど変わらないのであれば同じものとして扱ってもかまいません。 そうでないならば体積基準の濃度は、計算した質量分率から混合密度や混合分子量などを用いて変換すべきです。
(4)たとえば、1つの物質の流れでも、流れの移動をみるため色分けしたい場合があります。 そこで(2-4)式の拡散係数Di をゼロもしくはScを無限大にして計算することで流れにのって運ばれる分布がわかります。
このときの計算している変数をマーカー変数やパッシブスカラーといいます。
■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□
3.エネルギー方程式
熱力学第1則から得られる熱エネルギーのつりあい式は以下になります。
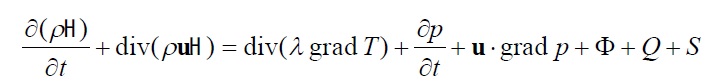 (3-1) (3-1)
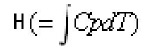 は密度平均された静エンタルピ、λ は熱伝導率です。右辺第一項は熱伝導に関するフーリエの法則に基づいた流体中の伝導による熱移動量を示したもの、右辺第二、第三は膨張・収縮による熱エネルギー変化分で
す。Q は単位体積あたり発(吸)熱量、S はエンタルピ生成を表します。 は密度平均された静エンタルピ、λ は熱伝導率です。右辺第一項は熱伝導に関するフーリエの法則に基づいた流体中の伝導による熱移動量を示したもの、右辺第二、第三は膨張・収縮による熱エネルギー変化分で
す。Q は単位体積あたり発(吸)熱量、S はエンタルピ生成を表します。
φ は粘性散逸項で以下になります。これは摩擦熱を意味しています。
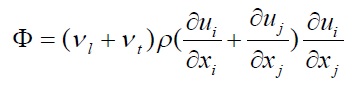 (3-2) (3-2)
ここでは式の細部よりもその形に関心を持って、いくつかの限定されたケースを考えます。定常低速流で粘性散逸を無視した場合、理想気体、固体、液体では熱エネルギー式は以下のようになります。? は温度拡散係数、Pr はプラントル数です。
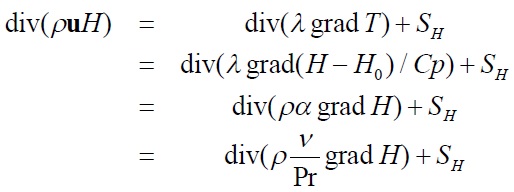 (3-3) (3-3)
上の2行目への変換は、H とT がCp について1対1の関係にあることから、
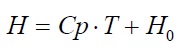 (3-4) (3-4)
であることを意味します。 H0 は化学反応や相変化を考えるとき重要な考え方です。
さらに、このことから従って全温の保存式は以下になります。
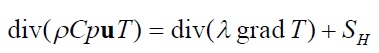 (3-5) (3-5)
熱流体解析ソフト「PHOENICS」では、本来保存量ではない温度を従属変数にとった場合、内部で自動的にCp をかけることでエネルギー保
存則を満足するようにしています。
この手法を用いると、全(静)エンタルピーと全(静)温度のいずれも従属変数に選ぶことができます。静エンタルピ、静温では、ビルトインソース項として(3-1)式の右辺2、3、4項が追加されます。
■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□■□
4.運動方程式
ニュートン流体において、ある方向における運動量の保存を支配する微分方程式も同様に表すことができます。 しかし、せん断応力及び垂直応力を考慮しなければならないうえ、ストークスの粘性則がフィックの法則やフーリエの法則より複雑なために、この微分方程式はより複雑になります。X方向速度成分をuとしてx方向の力のつりあいを考
えると次のような式が得られます。
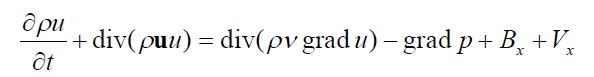 (4-1) (4-1)
ここで、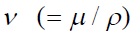 は動粘性係数、pは圧力、Bx はx方向の単位体積あたりの体積力、Vxは は動粘性係数、pは圧力、Bx はx方向の単位体積あたりの体積力、Vxは
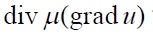 で示される以外の粘性散逸項を意味しています。 で示される以外の粘性散逸項を意味しています。
熱流体解析ソフト「PHOENICS」では、Vx は無視しています。また、Bx は重力や浮力など問題に応じてユーザーが指定することになります。
したがって自動的に組み込まれるビルトインソースは右辺第2項だけです。 ここで、直交もしくはBFC座標と円筒座標系のビルトインソース項を表に示します。
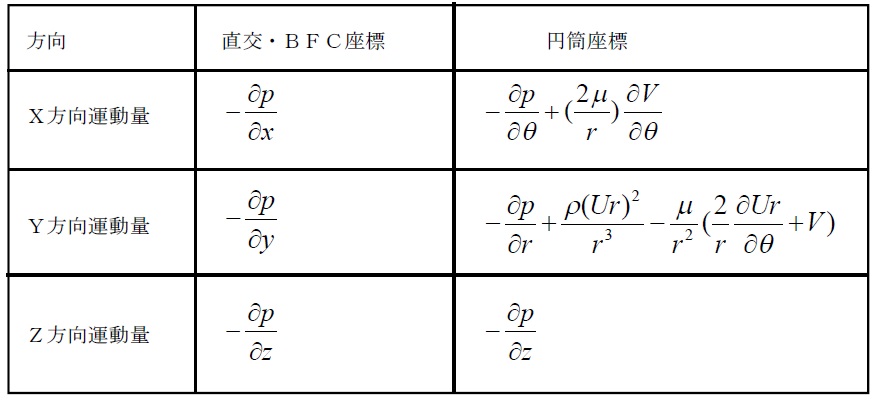
このように円筒座標系では遠心力が座標変換から自動的に組み込まれます。しかしコリオリ力は見かけの力であるので自動的に与えておらず、必要に応じて設定する特別なソースとして用意しています。
熱流体の流れの性質を決定するのは、左辺にあらわれる密度と右辺第1項の係数である粘度です。一方、流体の性質を表わすのに圧縮性/非圧縮性、ニュートン流体/非ニュートン流体という分類が良くされます。
圧縮性は、圧力による体積の変化を意味します。圧縮性流体は、(4−1)式を(3.1)式に代入したとき右辺第2項の
圧力勾配から得られるΔp/Δpを計算するとき、断熱膨張・収縮の関係から得られる
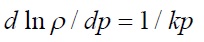
(k は比熱比)の分を付加します。 ユーザーは密度に状態方程式か等エントロピー変化の式を選びかつ、圧縮係数1/ k を与えることで表せます。したがって体積の変化は速度および密度の変化として表されることになります。
非ニュートン流体に関しては非常に広範囲になりますが、粘度をずり速度(流体の体積歪み)の関数で表すこと
が多いようです。 熱流体解析ソフト「PHOENICS」で組み込まれている非ニュートン流体の方法も動粘度を速度の関数にしています。
このように圧縮性や非ニュートン流体であっても、物性値が変わるだけで(4−1)式の形は変わりません。 |